Định lý Pytago và cách áp dụng định lý làm bài tập dễ hiểu nhất

Khi bạn bước vào chương trình trung học cơ sở, Định lý Pitago sẽ dạy bạn cách xác định độ dài các cạnh của một tam giác vuông. Vậy định lý này có khó không và cách sử dụng ra sao, các bạn cùng tìm hiểu bài viết sau nhé!

Ngày thứ nhấtĐịnh lý Pitago là gì?

Định lý Pitago là mối quan hệ cơ bản trong hình học Euclide giữa ba cạnh của một tam giác vuông. Định lý này được phát minh và đặt tên theo nhà toán học Hy Lạp cổ đại Pythagoras.

2Định lý Pythagore

câu

công thức nấu ăn

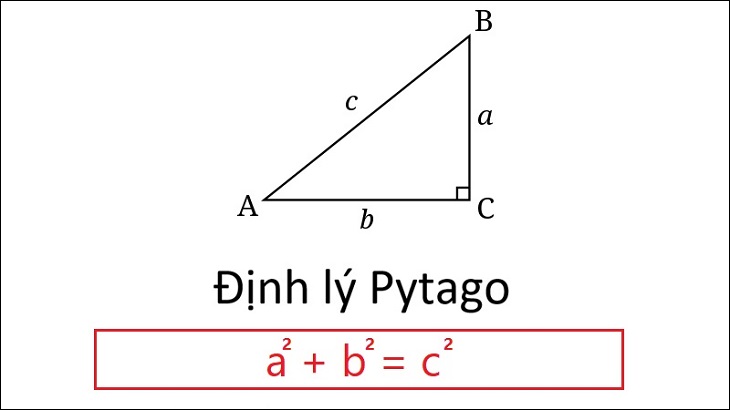
Ở trong:

• xa: Độ dài của hai cạnh góc vuông, còn được gọi là cạnh kề.
• NS.: Chiều dài cạnh huyền.

Chứng minh định lý

Nhà toán học Pitago đã chứng minh định lý sau bằng cách sắp xếp lại vị trí của các tam giác:

• Giả thuyết: Trong hai hình vuông lớn có diện tích bằng nhau, mỗi hình vuông chứa 4 hình tam giác có diện tích bằng nhau. Nếu chúng ta thay đổi vị trí của tam giác, chúng ta nhận được khoảng trống như hình bên.
• Có nguồn gốc từ: Diện tích các phòng ở hình vuông thứ nhất bằng tổng diện tích của hai phòng ở hình vuông thứ hai.

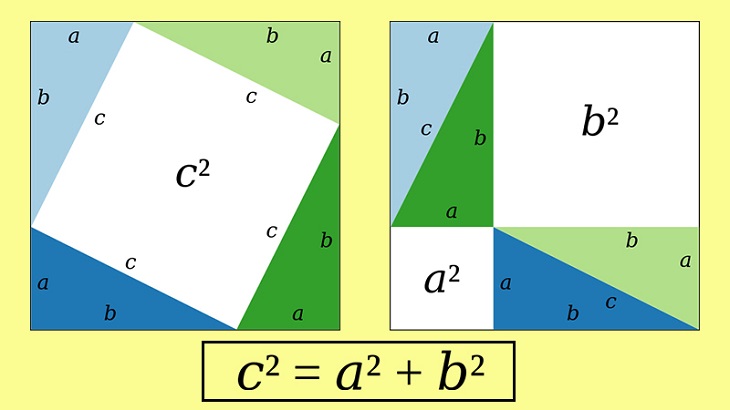
Bài tập minh họa

Đối tượng: Cho ABC là một tam giác nhọn. Vẽ đường cao AH vuông góc với BC (H thuộc BC). Có biết AB = 13 (cm), AH = 12 (cm), HC = 16 (cm). Tính độ dài các cạnh của tam giác ABC.

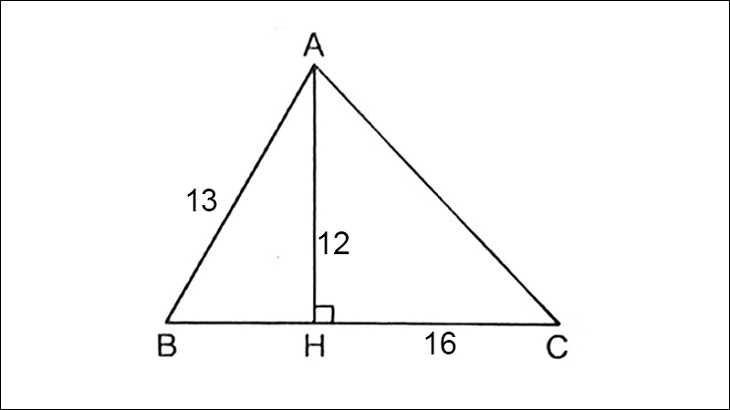
Câu trả lời:

– Trong tam giác AHC vuông góc với H, áp dụng:

AC² = AH² + HC² = 12² + 16² = 144 + 156 = 400 (cm)

=> AC = 20 (cm).

– Trong tam giác AHB, vuông góc với H, áp dụng:

áo lót² = AB² – AH² = 13² – thứ mười hai² = 169 – 144 = 25 (cm)

=> Áo ngực = 5 (cm).

=> BC = BH + HC = 5 + 16 = 21 (cm).

3Định lý nghịch đảo Pitago

câu

công thức nấu ăn

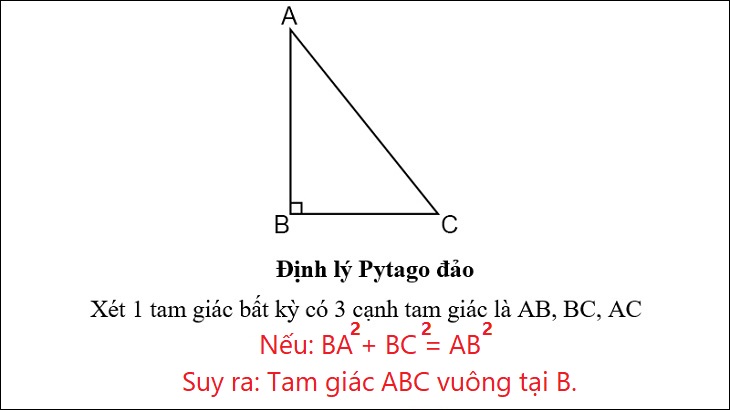
Chứng minh định lý

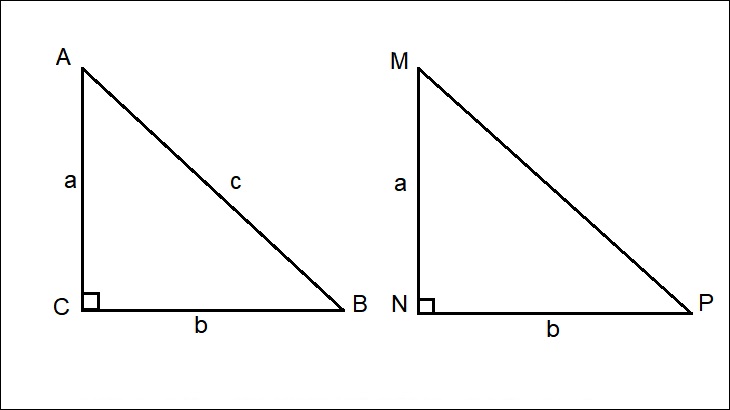
– Giả thiết ABC là tam giác có các cạnh a, b và c bằng Một² + b² = c²

– Dựng tam giác MPN thứ hai là tam giác vuông và các cạnh tạo bởi góc vuông này lần lượt là a và b.

Theo định lý thuận của Pythagoras, cạnh huyền của tam giác vuông là MPN. c = √(Một² + b²) và bằng cạnh còn lại của tam giác đầu tiên ABC. Điều này làm cho hai tam giác này đồng dư vì chúng có ba cạnh tương ứng tương ứng với độ dài của các cạnh a, b và c.

=> Góc giữa các cạnh a và b trong tam giác ABC là góc vuông.

theo dõi

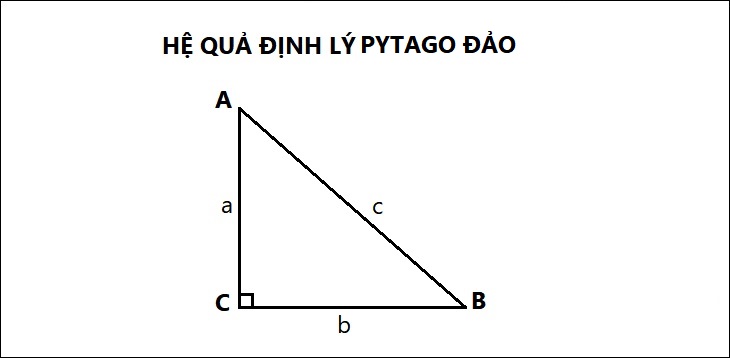
Định lý nghịch đảo Pitago giúp xác định xem một tam giác là vuông, nhọn hay tù. Tiến hành như sau:

– Gọi c là cạnh dài nhất của tam giác và có a + b> c (bất đẳng thức trong tam giác đối với sự tồn tại của tam giác).

Bài tập minh họa

Đối tượng: Cho ABC là tam giác có AB = 5, AC = 13, BC = 12. Chứng minh rằng tam giác ABC vuông góc với B.

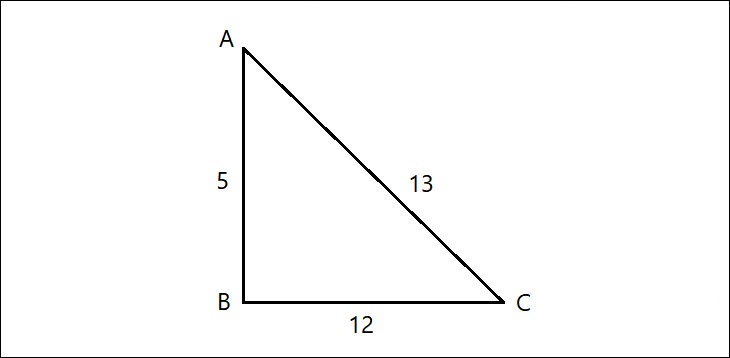
Câu trả lời:

– Với định lý nghịch đảo của Pythagoras ta có 5² + 12² = 13²

=> Tam giác ABC là tam giác vuông cân.

– Mặt khác AC = 13 cm có độ dài lớn nhất nên AC là cạnh huyền và đối diện với cạnh huyền là góc B vuông.

Do đó tam giác ABC vuông cân tại B.

lần thứ 4Bộ ba Pythagore nguyên thủy

Bộ ba Pitago nguyên thủy là ba số nguyên dương a, b và c. Chúng đại diện cho độ dài ba cạnh của một tam giác vuông và sẽ giúp bạn nhanh chóng suy ra độ dài của một cạnh nếu biết trước độ dài của hai cạnh kia.

Các bộ ba này thường được viết là (a, b, c). Dưới đây là 16 bộ ba phổ biến của Pitago: (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97).

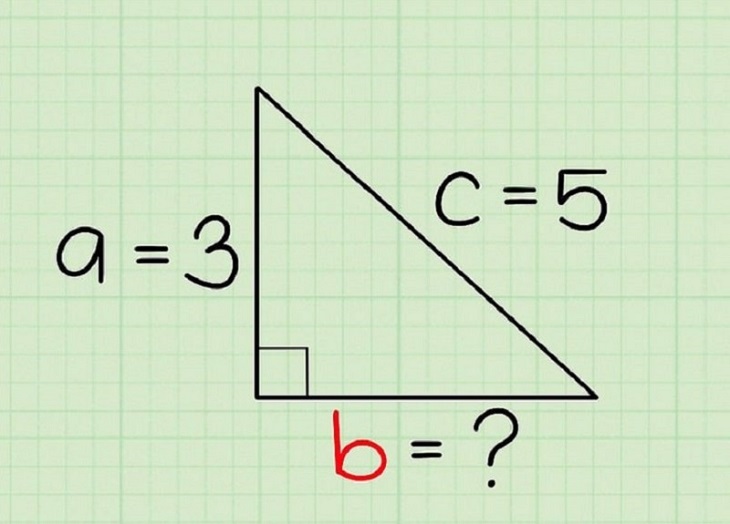
5Các bước sử dụng định lý tiến và lùi của Pythagoras

Các bước áp dụng định lý Pitago dương

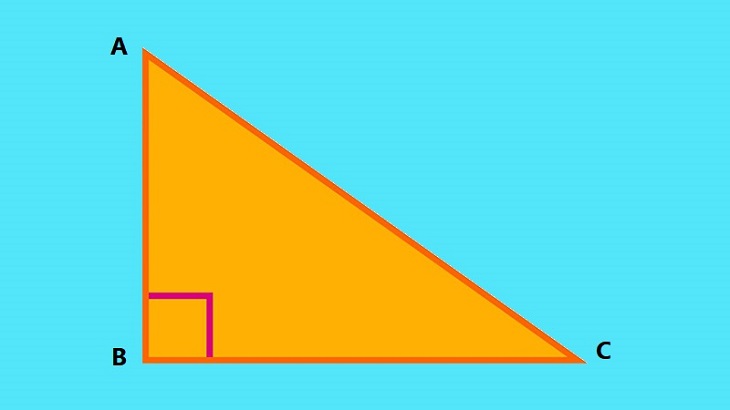
Bước 1: Xét một tam giác vuông có cạnh được tính.

Bước 2: Áp dụng định lý Pitago và đưa các số vào phương trình.

Bước 3: Tính độ dài cạnh đó để tìm ra kết luận.

Các bước áp dụng định lý nghịch đảo Pitago

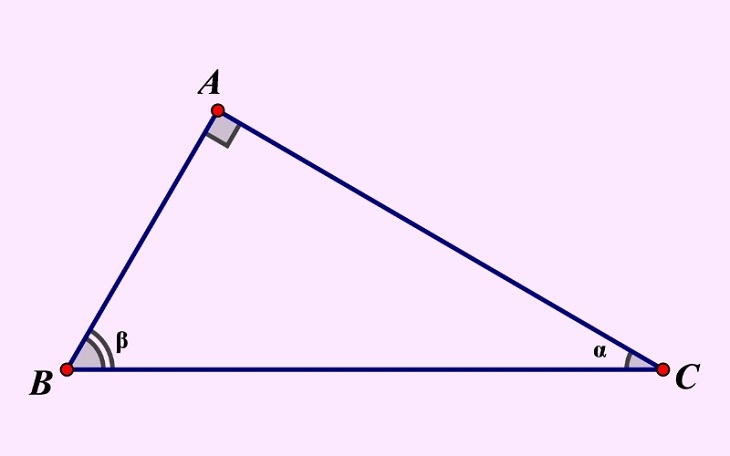
Bước 1: Chọn cạnh có chiều dài dài nhất và vuông nó.

Bước 2: Tìm tổng bình phương của hai cạnh còn lại.

Bước 3: So sánh và sử dụng định lý nghịch đảo Pitago để rút ra kết luận.

Ngày 6Bạn áp dụng định lý Pitago như thế nào?

Tính các cạnh của tam giác vuông

Bước 1: Gọi a và b là độ dài hai cạnh góc vuông và c là độ dài cạnh huyền.

Bước 2: Đặt độ dài các cạnh đã biết vào công thức Pitago.

Bước 3: Sử dụng công thức toán học để tính độ dài của cạnh còn lại.

Bài tập minh họa

Cho ABC là tam giác vuông tại A. Vẽ AH vuông góc với BC. Biết BH = 16 và HC = 9. Tính độ dài các cạnh của tam giác.

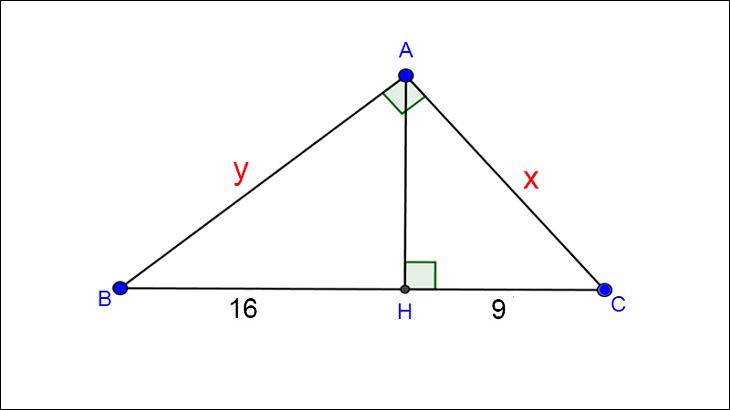
Câu trả lời

– Với định lí Pitago và hai tam giác vuông AHC và AHB ta được:

• NS² = AH² + 9² (Ngày thứ nhất)
• đúng² = AH² + 16² (2)

– Vì tam giác ABC ở A là góc vuông nên:

BC² = AB² + AC² = vâng² + x²

=> (9 + 16)² = (AH² + 16²) + (AH² + 9²)

=> 625 = AH thứ 2² + 337

=> AH² = 144

=> AH = 12 (cm)

– Thay AH = 12 vào (1), ta được x = 15 (cm)

– Thay AH = 12 vào (2), ta được y = 20 (cm)

Vậy độ dài cạnh AC = 15 (cm) và AB = 20 (cm).

Tính khoảng cách giữa 2 điểm trong mặt phẳng XY

Bước 1: Tìm hai điểm đã cho trong mặt phẳng XY. Trong đó (x1, y1) là điểm đầu tiên; (x2, y2) là điểm thứ hai.

Bước 2: Vẽ hai điểm trên sơ đồ. Đối với mỗi điểm, x là tọa độ trục hoành và y là tọa độ trục tung.

Bước 3: Tìm độ dài các cạnh của một góc vuông bằng công thức:

• | x1 – x2 | là chiều dài của cạnh ngang.
• | y1 – y2 | là chiều dài của cạnh thẳng đứng.

Bước 4: Sử dụng định lý Pitago để tính độ dài cạnh huyền.

Bài tập minh họa

Cho hai điểm A (5,2) và B (8,6). Tính độ dài cạnh huyền của tam giác ABC.

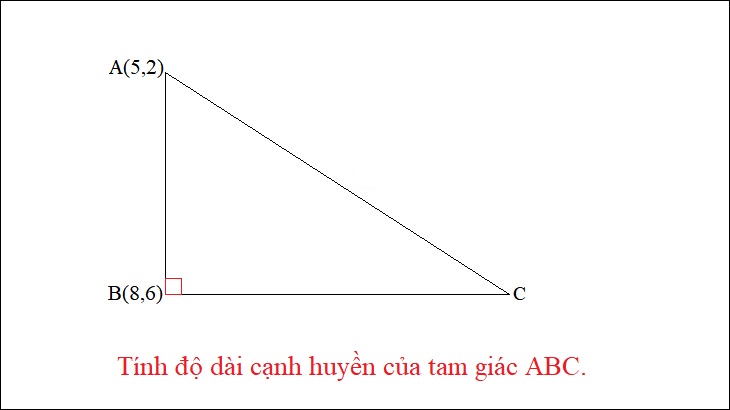
Câu trả lời:

Gọi a và b là độ dài hai cạnh góc vuông và c là độ dài cạnh huyền.

• Độ dài cạnh ngang: a = | x1 – x2 | = | 5 – 8 | = | -3 | = 3
• Độ dài cạnh đứng là: b = | y1 – y2 | = | 2 – 6 | = | -4 | = 4

Trong tam giác vuông này có 2 góc vuông, a = 3 và b = 4. Sử dụng bộ ba Pitago nguyên thủy, nhanh chóng suy ra cạnh huyền c = 5.

thứ 7Một số gợi ý về việc áp dụng định lý Pitago

Khi áp dụng định lý Pitago trong toán học, học sinh cần lưu ý những điểm sau:

• Định lý Pitago chỉ cho kết quả đúng khi áp dụng cho tam giác vuông.
• Để đảm bảo kết quả chính xác, hãy vẽ một hình tam giác trên giấy và ghi lại độ dài chính xác của các cạnh.
• Sử dụng định lý này, bạn chỉ có thể tính độ dài của cạnh thứ 3 nếu bạn biết độ dài của 2 cạnh còn lại.
• Khi tính căn bậc hai, bạn nên sử dụng máy tính bỏ túi để có kết quả chính xác.

Qua nội dung bài viết, Vzone hy vọng đã giúp bạn hiểu rõ hơn về định nghĩa và công thức của Định lý Pitago. Nếu bạn có thắc mắc gì về bộ sản phẩm này hãy để lại bình luận bên dưới nhé!