Công thức tính chu vi hình tam giác chi tiết nhất có ví dụ minh họa dễ hiểu

Công thức tính chu vi hình tam giác là một trong những công thức toán học mà các em cần nắm vững để dễ dàng vận dụng trong các bài tập. Bài viết dưới đây, Vzone chia sẻ bạn công thức tính chu vi hình tam giác với các ví dụ minh họa dễ hiểu.

Ngày thứ nhấtPhân loại hình tam giác

Theo độ dài của các cạnh

Theo độ dài các cạnh, người ta chia tam giác thành ba loại: tam giác đều, tam giác cân và tam giác đều.

Tam giác bình thường là một tam giác với ba chiều dài cạnh khác nhau, Đo ba góc khác nhau. Tuy nhiên, các tam giác đều cũng có thể chứa các trường hợp đặc biệt của một tam giác.

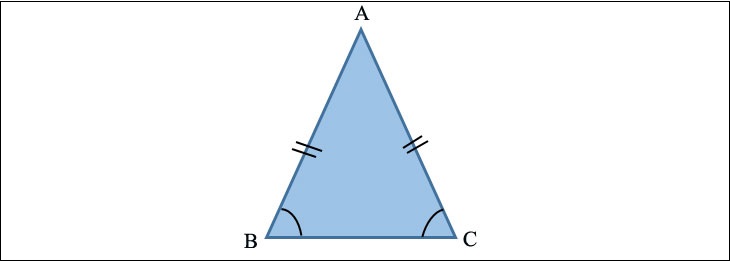
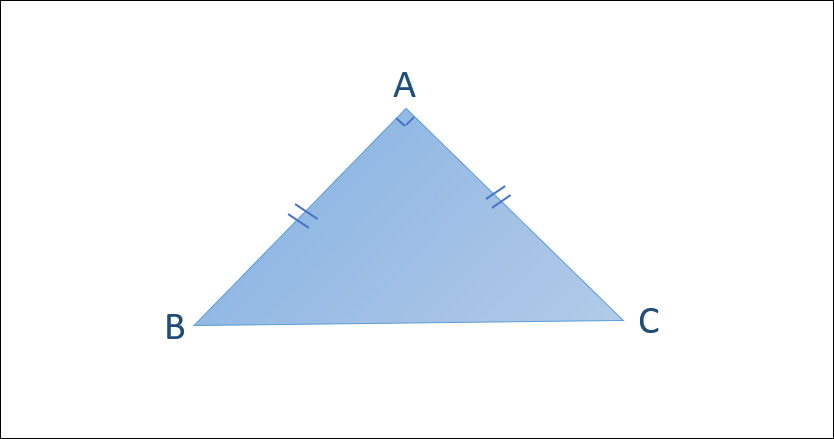
Tam giác cân là một tam giác với:

• Độ dài của hai cạnh là như nhau.
• Đỉnh của tam giác cân là giao điểm của hai cạnh.
• Góc tạo bởi đỉnh được gọi là góc đối đỉnh, và hai góc còn lại được gọi là góc cơ sở.
• Hai góc dưới là đồng dư.

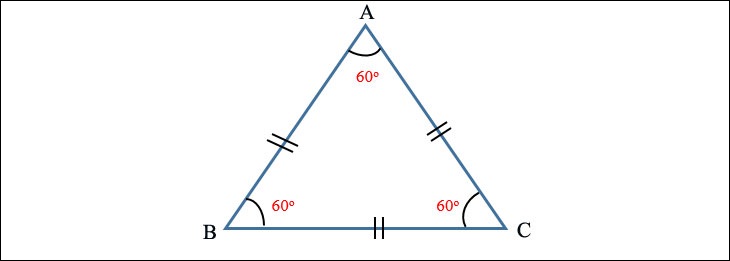
Tam giác đều là một trường hợp đặc biệt của tam giác cân mà độ dài của ba cạnh như nhau. Tính chất của tam giác đều là Đo từ ba góc bằng nhau và bằng 60 °.

Theo thước đo của góc nội thất

Phép chia theo số đo các góc trong bao gồm: tam giác nhọn, tam giác tù, tam giác vuông và tam giác vuông cân.

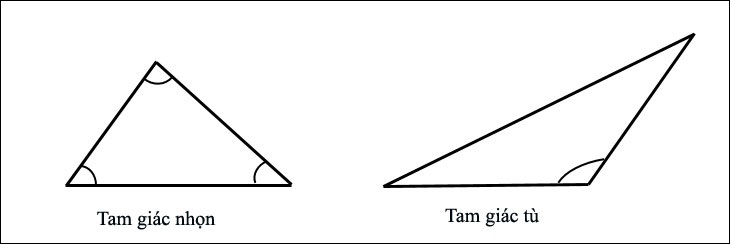
Tam giác nhọn là một tam giác với cả ba góc bên trong đều nhỏ hơn 90 ° (được gọi là ba góc nhọn) hoặc có tất cả Góc bên ngoài lớn hơn 90 ° (gọi là sáu góc tù).

Hình tam giác tù là một tam giác với một góc bên trong lớn hơn 90 ° (gọi là góc tù) hoặc có một góc bên ngoài nhỏ hơn 90 ° (một góc nhọn).

Tam giác vuông là một tam giác với một góc bằng 90 ° (gọi là góc vuông). Trong một tam giác vuông có:

• Cạnh đối diện với góc vuông được gọi là cạnh huyền, cũng là cạnh lớn nhất trong tam giác này.
• Hai cạnh còn lại gọi là góc vuông.

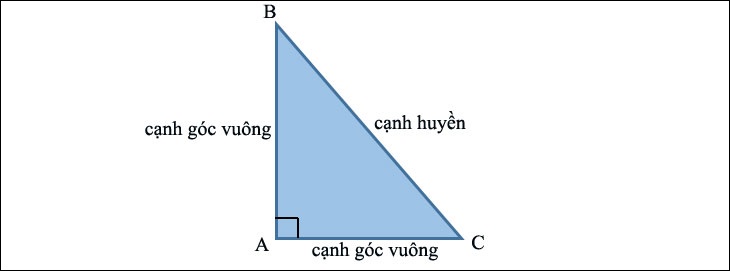
Góc vuông tam giác vừa là tam giác vuông vừa là tam giác cân. Trong một tam giác vuông cân là độ dài hai cạnh góc vuông giống nhau và mỗi cạnh góc nhọn là 45 °.

2Một số tính chất của hình tam giác

Dưới đây là một số tính chất của hình tam giác cần nhớ:

• Tổng các góc trong của một tam giác là 180 ° (tổng các góc trong của một tập hợp các tam giác).
• Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn. Ngược lại, góc đối diện với cạnh lớn hơn là góc lớn hơn (quan hệ giữa cạnh và góc đối diện trong tam giác).
• Độ dài mỗi cạnh của tam giác lớn hơn hiệu độ dài của hai cạnh còn lại và nhỏ hơn tổng của chúng (bất đẳng thức tam giác).
• Trong một tam giác, tỉ số độ dài của mỗi cạnh đối với sin của góc đối diện là như nhau đối với cả ba cạnh (định lý hàm số sin).
• Trong một tam giác, bình phương độ dài một cạnh bằng tổng bình phương độ dài hai cạnh kia trừ đi hai lần tích độ dài hai cạnh đó và côsin của góc giữa hai cạnh đó. (định lý hàm số cosin).

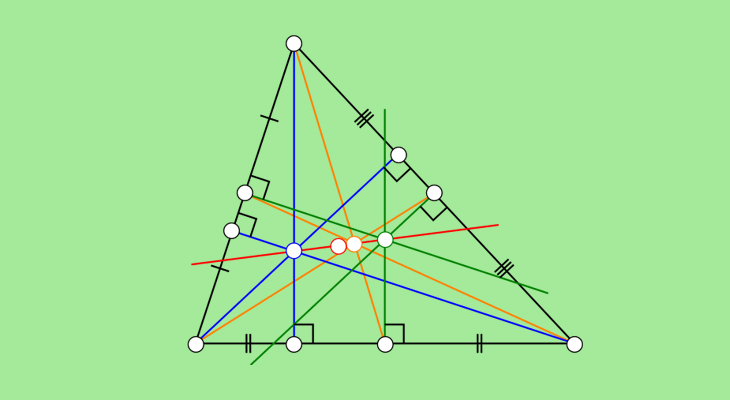
• Ba trung tuyến của một tam giác cắt nhau tại một điểm được gọi là trọng tâm của tam giác. Khoảng cách từ trọng tâm đến đỉnh của tam giác bằng 2/3 Độ dài trung vị. Đường trung tuyến của tam giác chia tam giác thành hai phần có diện tích bằng nhau (tam giác đồng dạng).
• Ba đường phân giác trong của tam giác cắt nhau tại một điểm và đó là tâm của đường tròn nội tiếp tam giác (tam giác đồng quy).
• Ba đường cao của tam giác cắt nhau tại một điểm và điểm này được gọi là trực tâm của tam giác (tam giác đồng quy).
• Ba đường trung trực của tam giác cắt nhau tại một điểm và điểm này là tâm đường tròn ngoại tiếp tam giác (tam giác cạnh).
• Trong một tam giác, đường phân giác chia cạnh đối diện thành 2 đoạn tỉ lệ với 2 cạnh kề.
• Đoạn giữa của tam giác song song với cạnh thứ ba và bằng một nửa độ dài của cạnh này (trung tuyến là đoạn thẳng nối các trọng tâm của hai cạnh của một tam giác, một tam giác có ba trung tuyến).

3Công thức tính chu vi hình tam giác

Chu vi của một tam giác bình thường

Chu vi hình tam giác thường bằng tổng độ dài ba cạnh của hình tam giác.

Ở trong:

• P: Chu vi của một tam giác thường.
• a, b, c: là độ dài ba cạnh của tam giác.

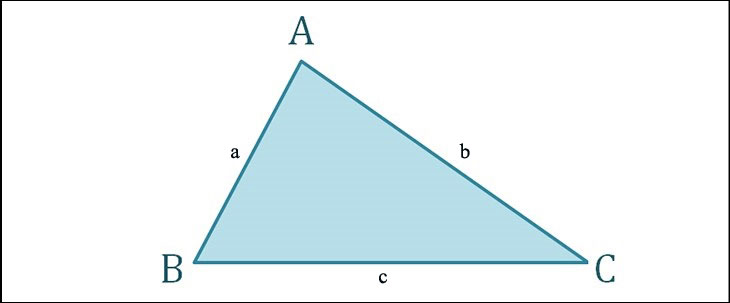
Ví dụ: Tìm chu vi tam giác ABC có độ dài các cạnh là: 5 cm, 8 cm và 9 cm.

Dạy:

Gọi a, b, c là độ dài ba cạnh của tam giác ABC.

Áp dụng công thức, ta có chu vi tam giác ABC là:

P = a + b + c = 5 + 8 + 9 = 22 (cm)

Chu vi tam giác vuông

Chu vi của một tam giác vuông bằng tổng độ dài hai cạnh và độ dài cạnh huyền của tam giác vuông đó.

Ở trong:

• P: Chu vi hình tam giác vuông.
• xa: Đây là độ dài hai cạnh của tam giác vuông.
• NS: Độ dài cạnh huyền của tam giác vuông.

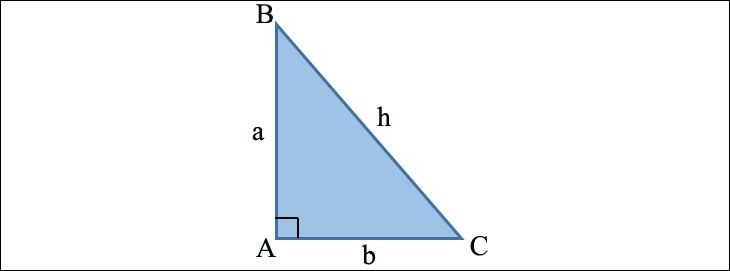
Ví dụ: Cho ABC là tam giác vuông tại A, độ dài cạnh huyền h = 9 cm, độ dài hai cạnh góc vuông là a = 7 cm và b = 5 cm. Bạn sẽ tính chu vi của tam giác vuông ABC?

Dạy:

Áp dụng công thức, ta có chu vi tam giác vuông ABC là:

P = a + b + h = 7 + 5 + 9 = 21 (cm).

Chu vi tam giác cân

Trước khi tính chu vi tam giác cân, bạn cần tìm đỉnh của tam giác cân và độ dài hai cạnh. Từ đó ta có thể tính chu vi của một tam giác cân là tích của độ dài hai cạnh cộng với đáy của tam giác.

Ở trong:

• P: Chu vi tam giác cân.
• Một: Kích thước chiều dài.
• NS: Chiều dài của cạnh dưới.

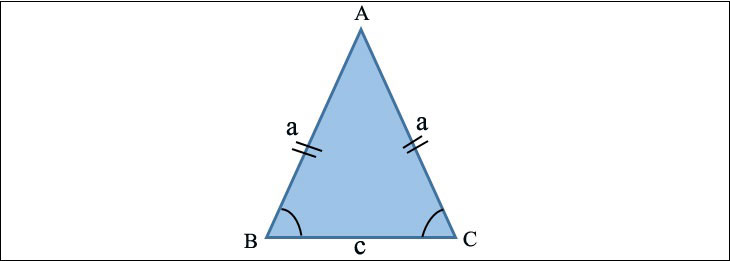
Ví dụ: Cho ABC là tam giác cân tại A, độ dài cạnh a = 9 cm và độ dài đáy c = 7 cm. Bạn có thể tìm chu vi của tam giác ABC?

Dạy:

Áp dụng công thức, ta có phạm vi của ABC là:

P = (2 * a) + c = (2 * 9) + 7 = 25 (cm).

Chu vi tam giác đều

Chu vi hình tam giác đều bằng độ dài một cạnh nhân với 3.

Ở trong:

• P: Chu vi hình tam giác đều.
• Một: Độ dài một cạnh của tam giác đều.

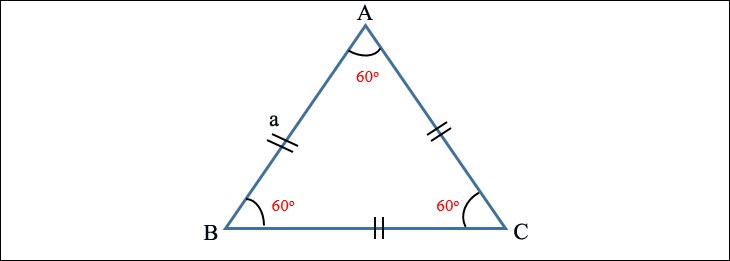
Ví dụ: Tìm chu vi của tam giác đều ABC có độ dài cạnh a = 7 cm.

Dạy:

Áp dụng công thức, ta có chu vi tam giác ABC là:

P = 3 * a = 3 * 7 = 21 (cm).

Chu vi của tam giác trong không gian

Ví dụ: Trong không gian cho mặt phẳng Oxy có hai điểm A (1; 3), B (4; 2).

A. Tìm tọa độ điểm D trên trục Ox sao cho DA = DB

B. Tính chu vi tam giác OAB?

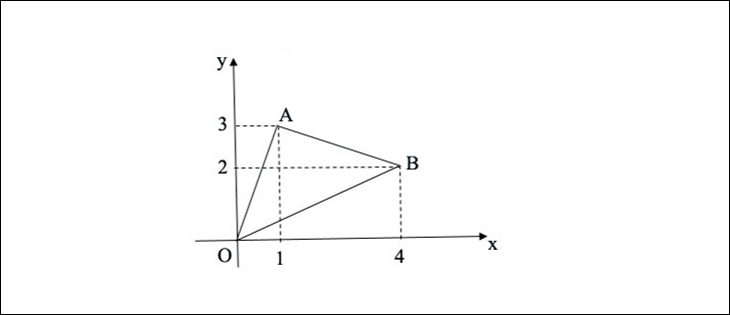
Dạy:

A. Ta có D trên trục tọa độ Ox

=> Tọa độ của D là: (x; 0)

DA² = (1-x) ² + 32

DB² = (4-x) ² + 2²

Theo chủ đề ta có: DA = DB => DA² = DB²

=> (1 – x) ² +9 = (4 – x) ² + 4

=> 6 * x = 10 => x = 5/3

Vậy tọa độ điểm D là D (5/3; 0)

B. Ta có: OA² = 1² + 3² = 10

=> OA = 10

ÜB² = 4² + 2² = 20

=> OB = 20

AB² = (4 – 1) ² + (2 – 3) ² = 10

=> AB = 10

Vậy chu vi tam giác OAB là:

P = OA + OB + AB = 10 + 20 + 10 = 10 * (2 + 2)

Bài viết tổng hợp các công thức tính chu vi hình tam giác với hình ảnh minh họa dễ hiểu. Mọi thắc mắc vui lòng để lại bình luận nhanh bên dưới để được hỗ trợ kịp thời!